深入浅出小青蛙过河

昨晚我的得意门生（四年级小男孩）给我发了一个“小青蛙过河，三分钟通过智商超群了！”的小程序。要和我比一比谁做得快，结果不出意料他赢了[害羞]。

我们最近在学习递归程序的编写，我总结了很多实例，其中有一个例子为汉诺塔。但我的例子都是引导孩子把问题不断分解，把子问题的答案不断合并，强调先分后合。对于复杂问题，我通常不让他们写代码只让他们画递归树。孩子说老师这个青蛙过河和汉诺塔很像，我都可以画出递归树，这个我有点出乎意料，这里来分享一下孩子的递归树。

汉诺塔递归树

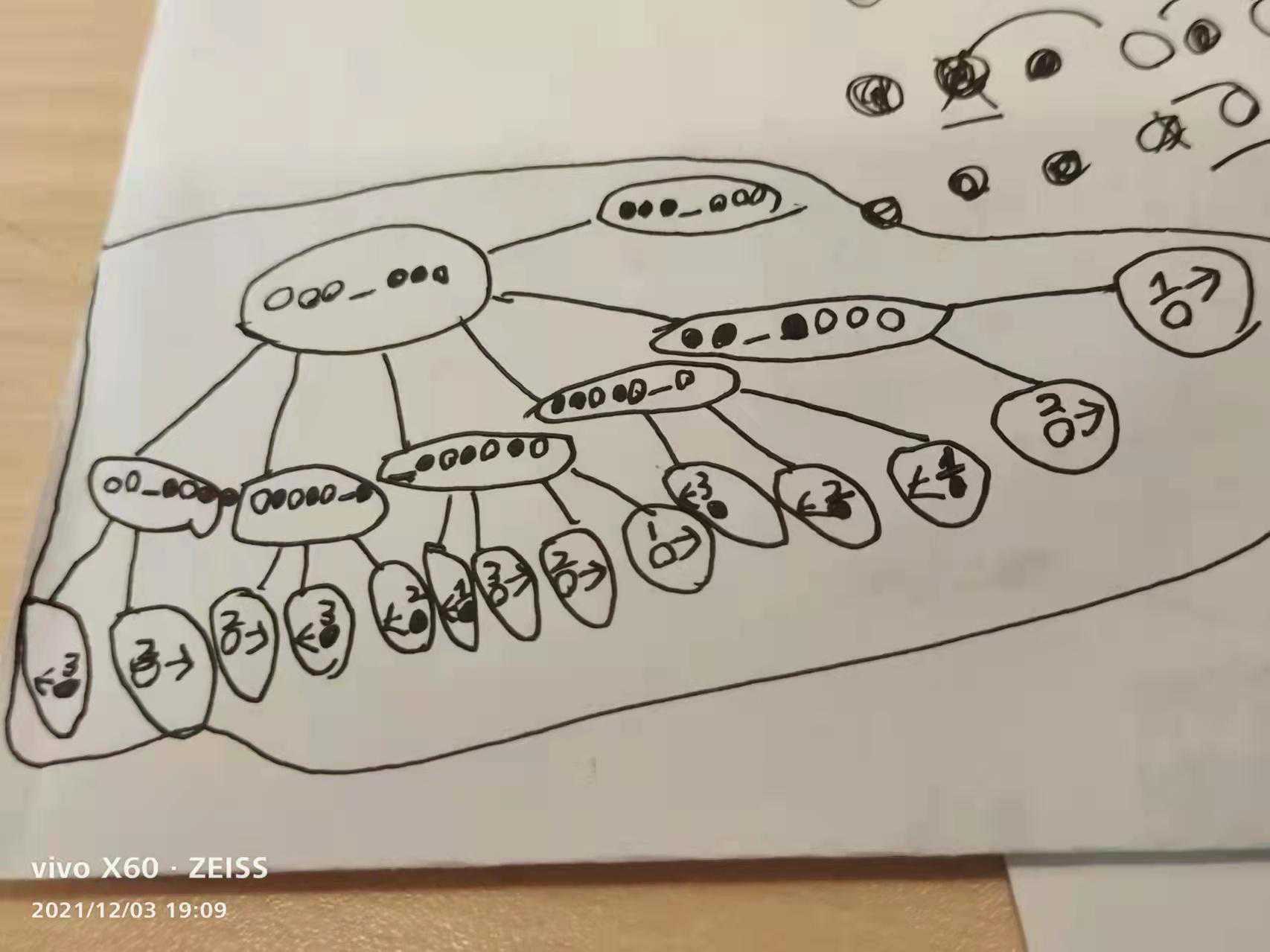
青蛙过河递归树

状态（ststus）：是对问题在某一时刻的进展情况的数学描述；

状态转移（state-transition）：是问题从一种状态转移到，另一种（或几种）状态的操作;

状态空间：搜索的目的实际上是在遍历一个隐式图，他的节点是所有的状态，有向边对应于状态的转移，而一个可行解就是一条从起始节点出发到达目标状态集中任意一个节点的路径。这样的图称为状态空间;

所以汉诺塔，八数码，甚至魔方其本质都是状态图搜索问题。

汉诺塔这个例子强调问题的分解与合并，递归处理同一问题不同的数据规模。目前还没有学习DFS呢，但没想到孩子悟出了DFS深度优先搜索和递归之间的微妙联系。

state=['绿','绿','绿','空','黄','黄','黄']target='黄黄黄空绿绿绿'dirs={'黄':'左','绿':'右'}规律2：黄青蛙只能向左，绿青蛙只能向右。#优化：记录无解的状态，预判无解，进行剪枝~ans=[]defsolve(state,ans):if''.join(state)==target:print("一组解为：")foreleinans:print(ele)returnidx=('空')fori,jin[(-2,'绿'),(-1,'绿'),(1,'黄'),(2,'黄')]:ifidx+ilen(state)andidx+i=0:ifstate[idx+i]==j:state[idx+i],state[idx]='空',(f"位置{1+idx+i}上的{j}色青蛙向{dirs[j]}跳{abs(i)}步")solve(state,ans)()state[idx],state[idx+i]='空',jsolve(state,ans)

通过编程求解，我们发现一共有两个合法的解，如下图所示：

解一

解二