今天,我们来教AI下国际象棋

国际象棋可以说是最棒的棋盘游戏之一,它是战略战术和纯技术的完美融合。每位玩家开局时各有16枚棋子:一王、一后、两车、两马、两象和八兵,各具不同功能与走法。真人对弈可以凭借玩家的经验,步步为营。那么,对于一个机器——计算机,你该如何教会它下棋?近日,有人在medium上发表了一篇文章,详细解释了如何教计算机玩国际象棋。
本文将从5个方面进行介绍:
Board表示;
Board评估;
移动选择;
测试AI;
接口测试。
在开始之前,你只需要提前安装Python3。
Board表示
首先,你需要对棋子背后的逻辑进行编码,即为每个棋子分配每一次可能的合法移动。
python-chess库为我们提供了棋子的移动生成和验证,简化了工作,安装方式如下:
!pipinstallpython-chess
python-chess库安装好后,导入chess模块并进行初始化:
importchessboard=()board
在notebook中的输出如下所示:
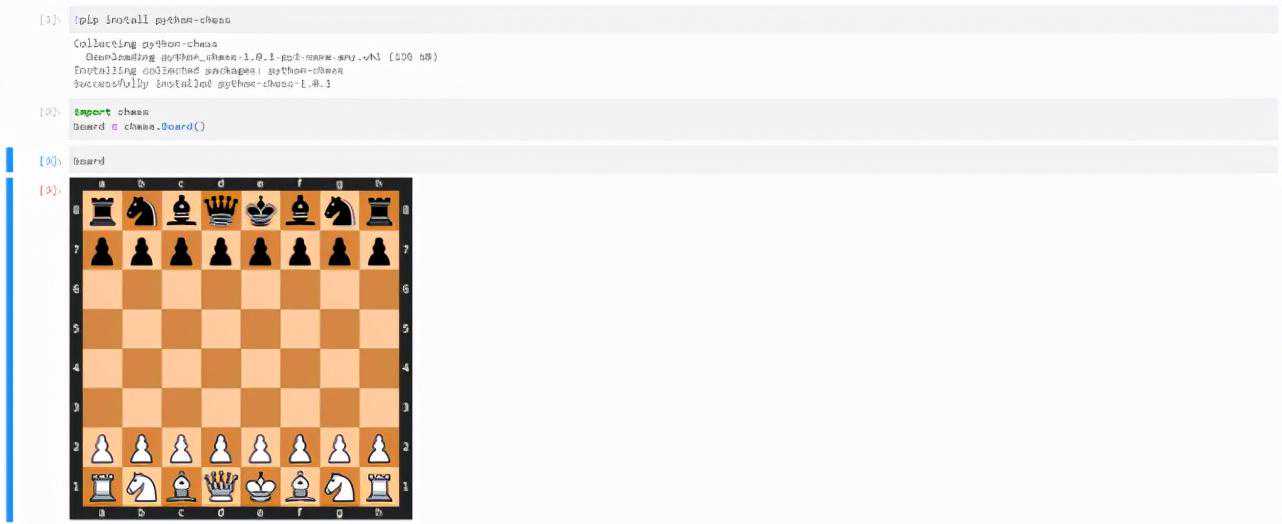
board对象是一个完整的board表示,该对象为我们提供了一些重要的函数,例如,_checkmate()函数检查是否存在将杀(checkmate),()函数附加一个移动,()函数撤销最后一次移动等。阅读完整的文档请参阅:
Board评估
为了对board进行初步评估,必须考虑一位大师在各自比赛中的想法。
我们应该想到的一些要点是:
避免用一个小棋子换三个兵;
象总是成对出现;
避免用两个小棋子换一辆车和一个兵。
将上述要点以方程形式进行表达:
象3个兵马3个兵;
象马;
象+马车+兵。
通过化简上述方程,可以得到:象马3个兵。同样,第三个方程可以改写成:象+马=车+1.5个兵,因为两个小棋子相当于一个车和两个兵。
使用piecesquaretable来评估棋子,在8x8的矩阵中设置值,例如在国际象棋中,在有利的位置设置较高的值,在不利的位置设置较低的值。
例如,白色国王越过中线的概率将小于20%,因此我们将在该矩阵中将数值设置为负值。
再举一个例子,假设皇后希望自己被放在中间位置,因为这样可以控制更多的位置,因此我们将在中心设置更高的值,其他棋子也一样,因为国际象棋都是为了保卫国王和控制中心。
理论就讲这些,现在我们来初始化piecesquaretable:
pawntable=[0,0,0,0,0,0,0,0,5,10,10,-20,-20,10,10,5,5,-5,-10,0,0,-10,-5,5,0,0,0,20,20,0,0,0,5,5,10,25,25,10,5,5,10,10,20,30,30,20,10,10,50,50,50,50,50,50,50,50,0,0,0,0,0,0,0,0]knightstable=[-50,-40,-30,-30,-30,-30,-40,-50,-40,-20,0,5,5,0,-20,-40,-30,5,10,15,15,10,5,-30,-30,0,15,20,20,15,0,-30,-30,5,15,20,20,15,5,-30,-30,0,10,15,15,10,0,-30,-40,-20,0,0,0,0,-20,-40,-50,-40,-30,-30,-30,-30,-40,-50]bishopstable=[-20,-10,-10,-10,-10,-10,-10,-20,-10,5,0,0,0,0,5,-10,-10,10,10,10,10,10,10,-10,-10,0,10,10,10,10,0,-10,-10,5,5,10,10,5,5,-10,-10,0,5,10,10,5,0,-10,-10,0,0,0,0,0,0,-10,-20,-10,-10,-10,-10,-10,-10,-20]rookstable=[0,0,0,5,5,0,0,0,-5,0,0,0,0,0,0,-5,-5,0,0,0,0,0,0,-5,-5,0,0,0,0,0,0,-5,-5,0,0,0,0,0,0,-5,-5,0,0,0,0,0,0,-5,5,10,10,10,10,10,10,5,0,0,0,0,0,0,0,0]queenstable=[-20,-10,-10,-5,-5,-10,-10,-20,-10,0,0,0,0,0,0,-10,-10,5,5,5,5,5,0,-10,0,0,5,5,5,5,0,-5,-5,0,5,5,5,5,0,-5,-10,0,5,5,5,5,0,-10,-10,0,0,0,0,0,0,-10,-20,-10,-10,-5,-5,-10,-10,-20]kingstable=[20,30,10,0,0,10,30,20,20,20,0,0,0,0,20,20,-10,-20,-20,-20,-20,-20,-20,-10,-20,-30,-30,-40,-40,-30,-30,-20,-30,-40,-40,-50,-50,-40,-40,-30,-30,-40,-40,-50,-50,-40,-40,-30,-30,-40,-40,-50,-50,-40,-40,-30,-30,-40,-40,-50,-50,-40,-40,-30]
通过以下四种方法得到评估函数:
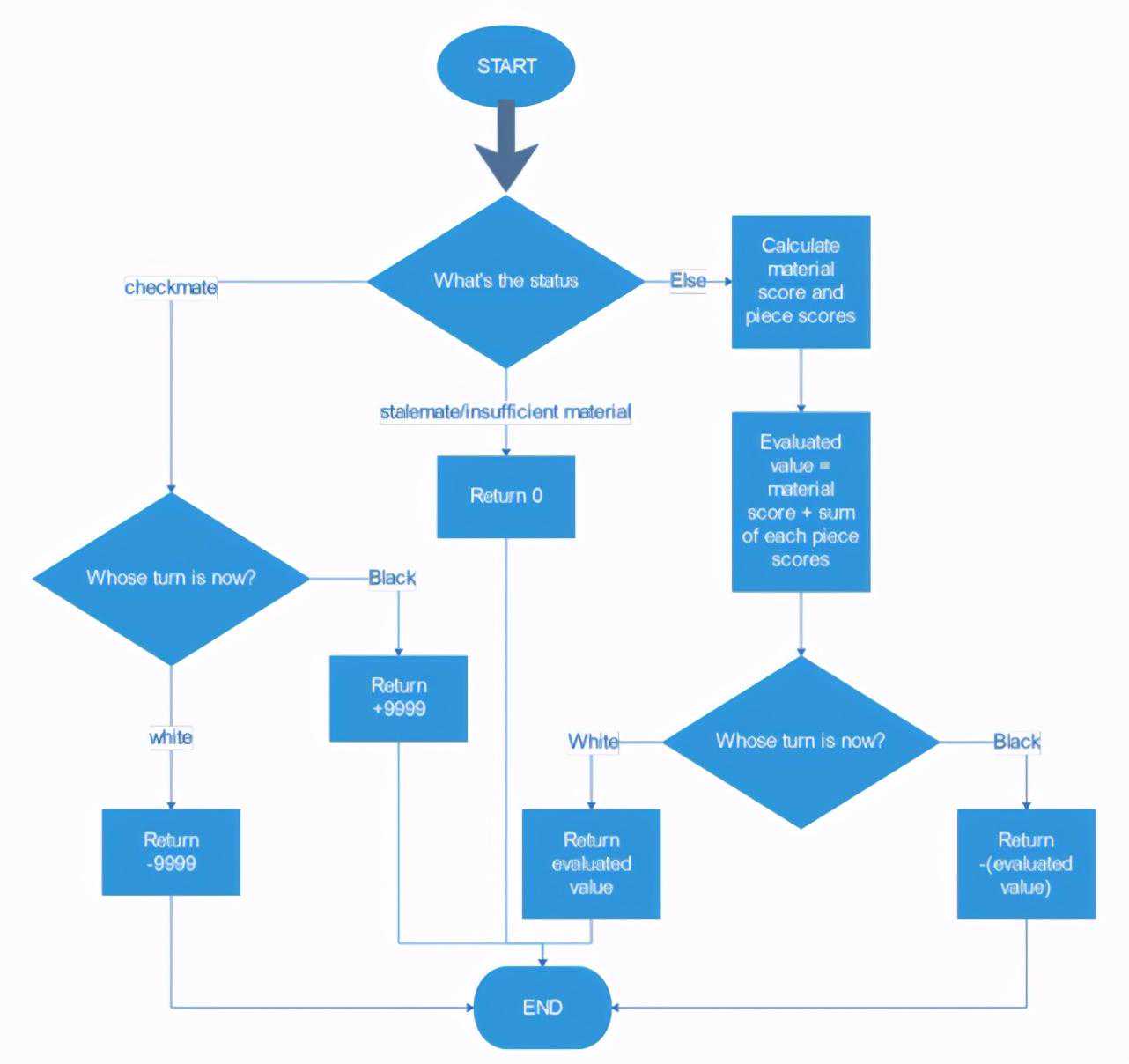
第一步检查游戏是否还在继续。
这个阶段的背后编码逻辑是:如果它在checkmate时返回true,程序将会检查轮到哪方移动。如果当前轮到白方移动,返回值为-9999,即上次一定是黑方移动,黑色获胜;否则返回值为+9999,表示白色获胜。对于僵局或比赛材料不足,返回值为0以表示平局。
代码实现方式:
_checkmate()::return-9999else:_stalemate():_insufficient_material():return0
第二步,计算总的棋子数,并把棋子总数传递给material函数。
wp=len((,))bp=len((,))wn=len((,))bn=len((,))wb=len((,))bb=len((,))wr=len((,))br=len((,))wq=len((,))bq=len((,))
第三步,计算得分。material函数得分的计算方法是:用各种棋子的权重乘以该棋子黑白两方个数之差,然后求这些结果之和。而每种棋子的得分计算方法是:该棋子在该游戏实例中所处位置的piece-square值的总和。
material=100*(wp-bp)+320*(wn-bn)+330*(wb-bb)+500*(wr-br)+900*(wq-bq)pawnsq=sum([pawntable[i](,)])pawnsq=pawnsq+sum([-pawntable[_mirror(i)](,)])knightsq=sum([knightstable[i](,)])knightsq=knightsq+sum([-knightstable[_mirror(i)](,)])bishopsq=sum([bishopstable[i](,)])bishopsq=bishopsq+sum([-bishopstable[_mirror(i)](,)])rooksq=sum([rookstable[i](,)])rooksq=rooksq+sum([-rookstable[_mirror(i)](,)])queensq=sum([queenstable[i](,)])queensq=queensq+sum([-queenstable[_mirror(i)](,)])kingsq=sum([kingstable[i](,)])kingsq=kingsq+sum([-kingstable[_mirror(i)](,)])
第四步,计算评价函数,此时将会返回白棋的material得分和各棋子单独得分之和。
eval=material+pawnsq+knightsq+bishopsq+rooksq+queensq+:returnevalelse:return-eval
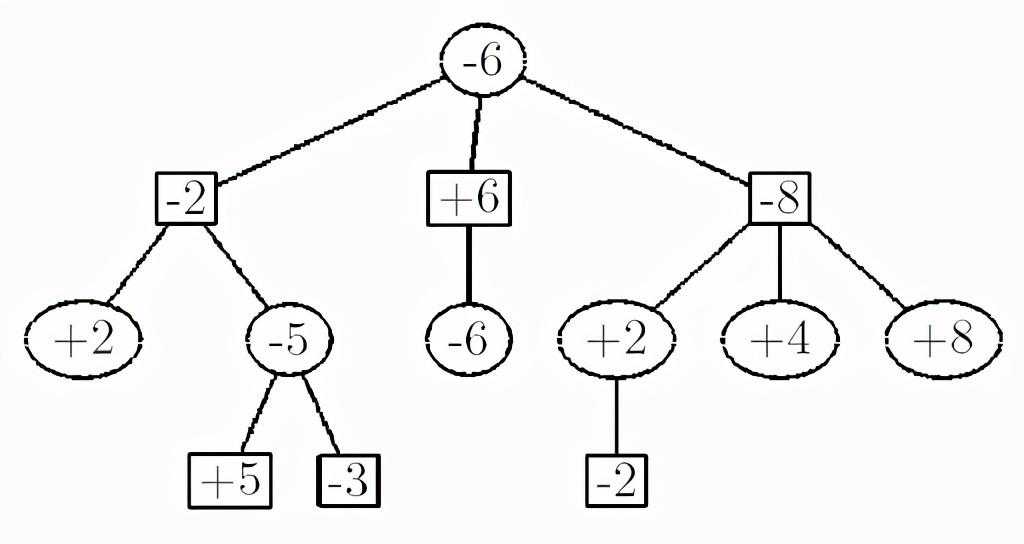
评价函数流程图
移动选择
算法的最后一步是用Minimax算法中的Negamax实现进行移动选择,Minimax算法是双人游戏(如跳棋等)中的常用算法。之后使用Alpha-Beta剪枝进行优化,这样可以减少执行的时间。
现在让我们深入研究一下minimax算法。该算法被广泛应用在棋类游戏中,用来找出失败的最大可能性中的最小值。该算法广泛应用于人工智能、决策论、博弈论、统计和哲学,力图在最坏的情况下将损失降到最低。简单来说,在游戏的每一步,假设玩家A试图最大化获胜几率,而在下一步中,玩家B试图最小化玩家A获胜的几率。
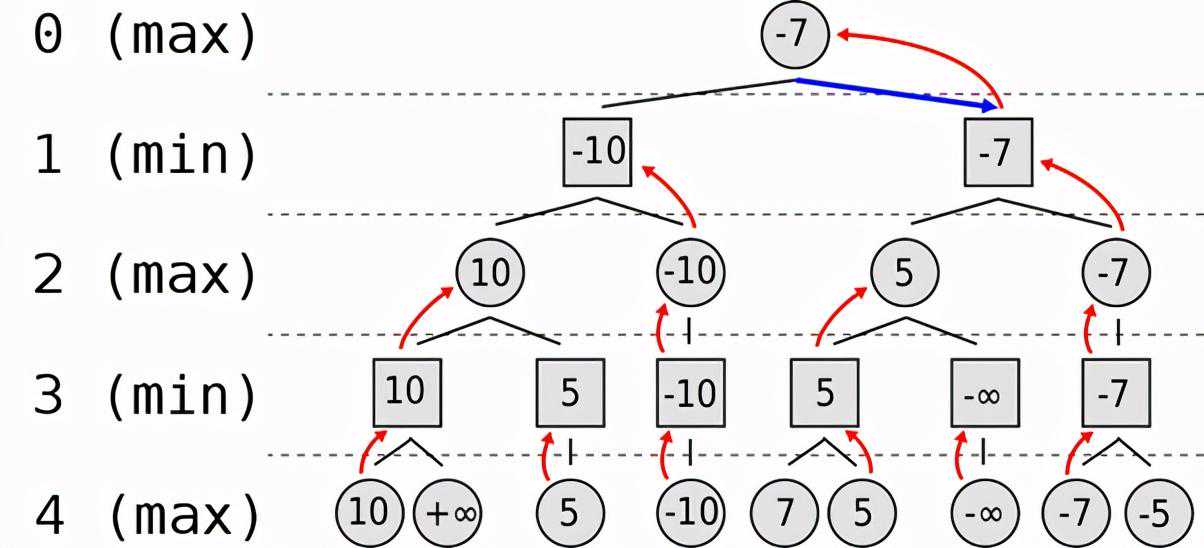
为了更好地理解minimax算法,请看下图:
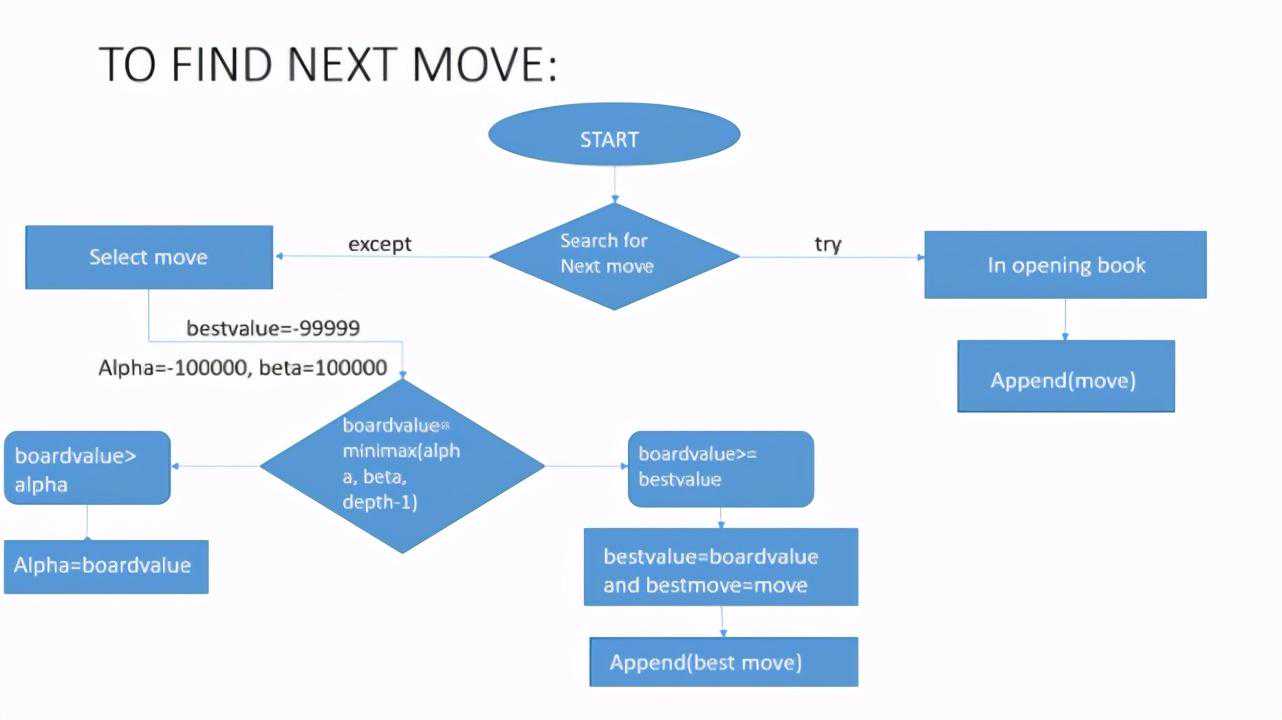
维基百科中minimax树举例
为了得到更好的结果,使用minimax变体negamax,因为我们只需要一个最大化两位玩家效用的函数。不同点在于,一个玩家的损失等于另一个玩家的收获,反之亦然。
就游戏而言,给第一个玩家的位置值和给第二个玩家的位置值符号是相反的。
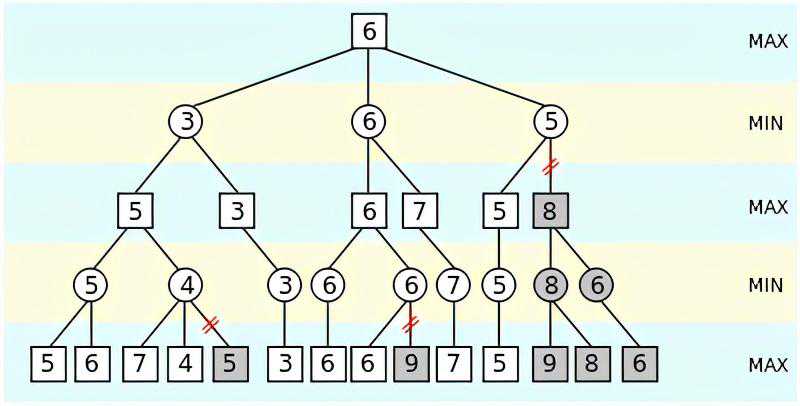
negamax示例
首先,我们将alpha设为负无穷大,beta设为正无穷大,这样两位玩家都能以尽可能差的分数开始比赛,代码如下:
except:bestMove=()bestValue=-99999alpha=-100000beta=100000_moves:(move)boardValue=-alphabeta(-beta,-alpha,depth-1)ifboardValuebestValue:bestValue=boardValuebestMove=moveif(boardValuealpha):alpha=()returnbestMove
下面让我们以流程图的方式来解释:
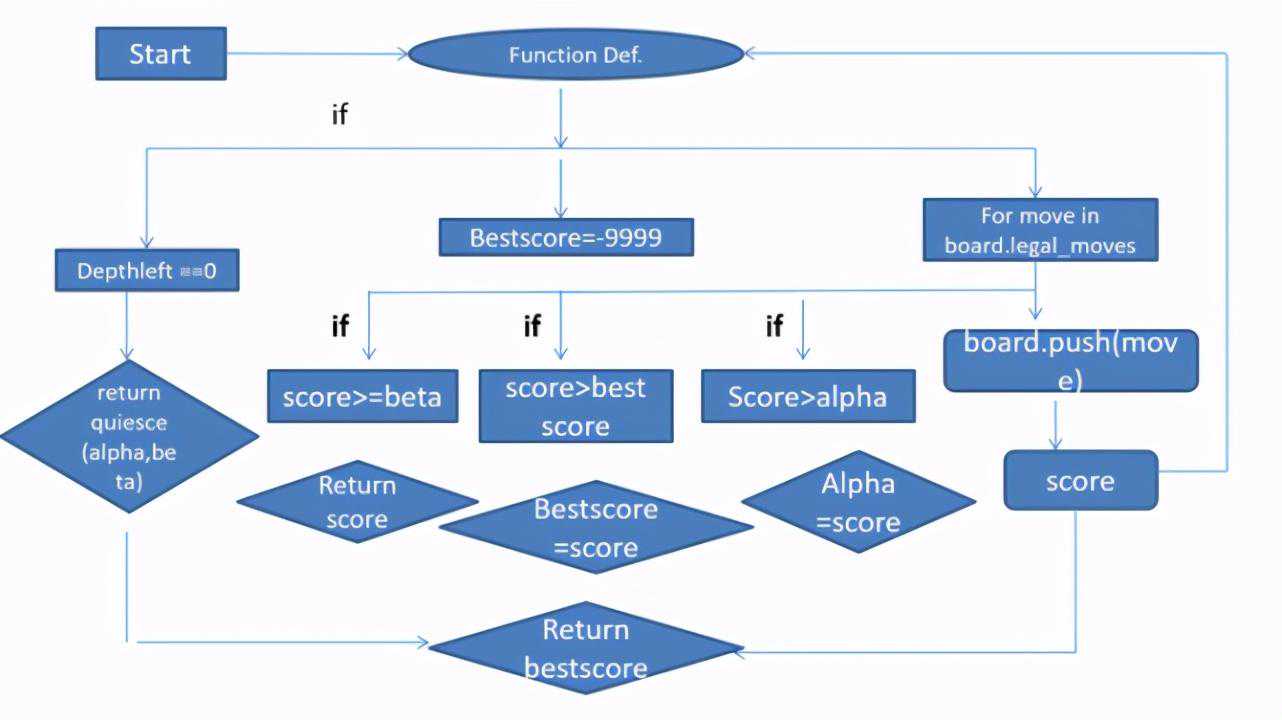
search函数的流程图
下一步是进行alpha-beta的剪枝来优化执行速度。
来自维基百科的alpha-beta剪枝说明
代码如下:
defalphabeta(alpha,beta,depthleft):bestscore=-9999if(depthleft==0):returnquiesce(alpha,beta)_moves:(move)score=-alphabeta(-beta,-alpha,depthleft-1)()if(score=beta):returnscoreif(scorebestscore):bestscore=scoreif(scorealpha):alpha=scorereturnbestscore
现在,让我们用下面给出的流程图来调整alphabeta函数:

现在是静态搜索,这种搜索旨在仅评估静态位置,即不存在致胜战术移动的位置。该搜索需要避免由搜索算法的深度限制所引起的水平线效应(horizoneffect)。
代码如下:
defquiesce(alpha,beta):stand_pat=evaluate_board()if(stand_pat=beta):returnbetaif(alphastand_pat):alpha=stand__moves:_capture(move):(move)score=-quiesce(-beta,-alpha)()if(score=beta):returnbetaif(scorealpha):alpha=scorereturnalpha
简单总结一下quiesce函数:

quiesce函数流程图。
测试AI
开始测试前,需要导入一些库:
测试有3项:
AI对弈人类;
AI对弈AI;
AI对弈Stockfish。
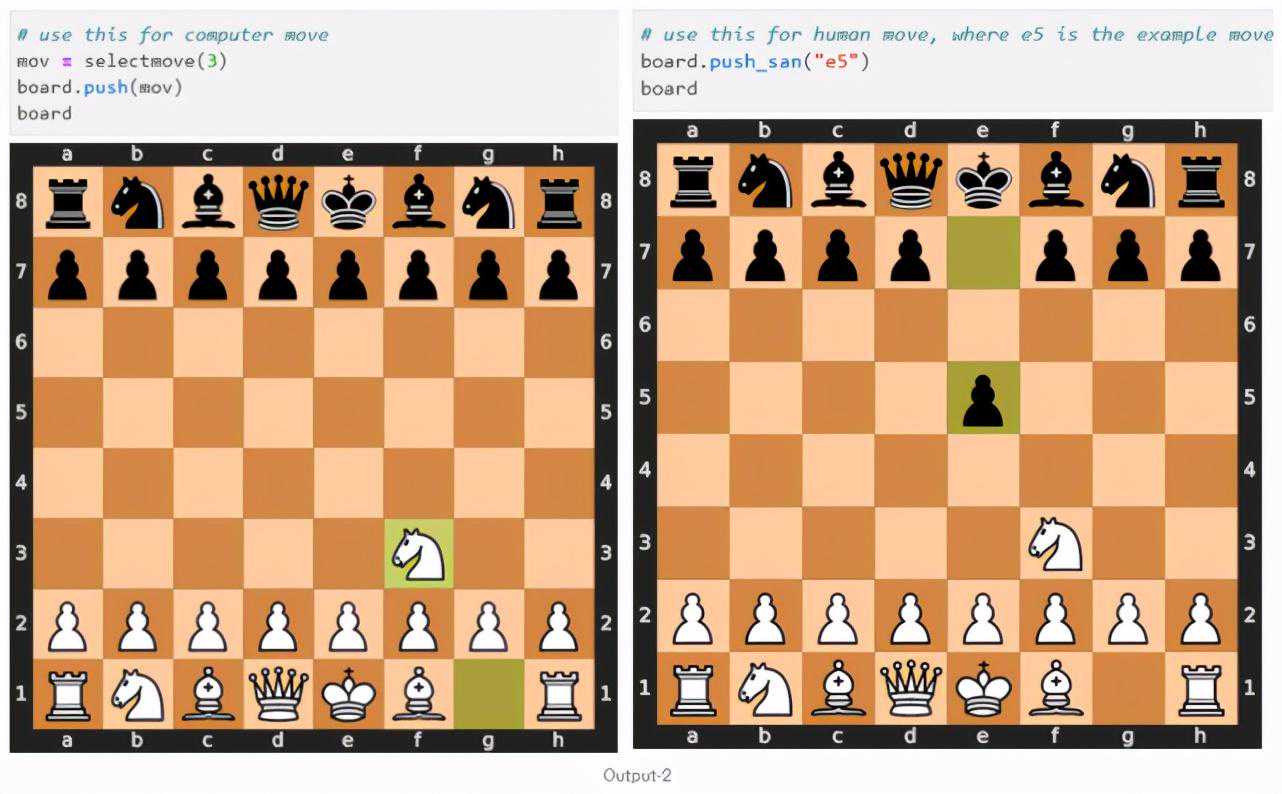
1.AI对弈人类:
AI选择从g1到f3,这是一个很明智的选择。
2.AI对弈AI:
3.AI对弈Stockfish:
可以得出:AI还不够智能,不足以打败stockfish12,但仍然坚持走了20步。
接口测试
上述测试方式看起来代码很多,你也可以写一个接口测试AI。
然后执行:
最终输出
推荐阅读
-
查叫两家应该也可以了#四川麻将
没牌胡,幺鸡四翻起胡七翻满。这个桶清跟我真太有缘了,这把又是一把做桶清的牌,一圈下来下家和对家缺桶,上家和我缺条,这牌现在就想往大单吊打。上家连打了一对8筒,看这个架势是我们一家收筒,对家清一色双根杠开了,不知道满没满。这里其实我可以直接杠下去,但是我觉得杠开了我也不想走,所以我就还是继续退了手。上...
-
汪小菲马筱梅接受媒体采访,提到婚礼、孩子等话题
这段时间,汪小菲和大S在经过激烈的纷争之后,似乎转入了另一赛道继续竞争。从法庭到警局,汪小菲的“湾囧”之旅令他身心俱疲。回到北京,汪小菲晒照宣布向女友马筱梅求婚成功,并晒出硕大的求婚钻戒,据说,正是大S结婚时想要刷汪小菲的购买,结果付款失败的那一款。汪小菲的壕气让大S手上的刺青戒指瞬间就不香了。双方...
-
《SUP 多人赛车》:手残玩了笑出声,多人赛车竞速竟然还能这么玩?
说到赛车竞速游戏大家第一反应应该就是移动平台极具人气的经典传统赛车作品《狂野飙车》和《极品飞车》了,这类游戏通过逼真的场景和精细的操作给玩家带来惊险刺激的感受。但是近年来,玩家也越来越多元化,很多赛车游戏也开始走一些操作简单、交互性强的游戏风格,而这类游戏因为操作简单,所以也更像是休闲游戏。今天给大...
-
七夕搭鹊桥,单身青年小游戏中牵手
新京报快讯(记者吴婷婷)七夕传统游戏、才艺展示、“爱情车票”……今天(8月25日)晚上7点7分,大兴区亦庄镇的80多位姑娘、小伙在七夕游戏中了解彼此。同时,在北京经开区,约50名来自各企业的单身青年汇聚一堂,在小游戏中相互认识。今晚,在经开区和大兴区亦庄镇,两个七夕活动分别进行。“我们是去年牵手成功...